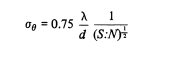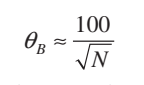Generations are all well and good, but how much of an actual detection ability difference does it translate into, especially against small LO targets like cruise missiles?
Range wise tho.. if you only count the power.. not much. Twice the power is 19%. It's easy to calculate with 4th root law.
Rfactor=(Pscale/Preference)^(1/4)
Where Pscale is your scaled power factor, say twice, thrice, hundreds
Preference is your baseline power value
Suppose we have Increase in power by factor of say 2 as my example, it would be :
Rfactor = (2/1)^(1/4)
Rfactor = 1.18 times the range of the earlier radar.
So ideally the new GaN radar would detect same target 1.18 times longer compared to the GaAs radar. Now assume 5 times increase in power, you can repeat the calculation and found factor of 1.5.
Tho naturally with more power comes more heat, especially if your amplifier is biased as A class, the most linear but also the least efficient in PAE (Power Added Efficiency) Thus more cooling. With typical PAE of some 30-35%. I usually assumed 33% based on book "Transmit Receive Module for Radars and Communications system". If AB or lower classes like B,C,D and E can be acceptable, much better PAE can be achieved.
----
The other thing comes with more power tho is better SNR (Signal To Noise Ratio), means better angular accuracy. For a swerling case-1 target with say False alarm rate of 10^-6, SNR of 13 dB (20 in dimensionless format) are needed, a textbook value one can find in most radar books (e.g Skolnik or Adamy). Now suppose a radar can achieve that SNR in a range, say 200 km against a target, now a radar with GaN module having say 5 times the power, what kind of SNR you can achieve at the same distance ?
Yet another form of 4th root law can be used.
SNRsc=SNRref*(Psc/Pref)*((Rref/Rsc)^4)
Where Rsc is your scaled range can be any value, as long as its consistent preferrably meters Rref is your baseline reference range, if you wonder why it's to the power of 4, it's because deriviation of radar range equation from a "single path" Friis Transmission equation which basically for radar, signal travels twice (transmit and receive) Hence factor of 4 for SNR or fourth root to find the range. Since we want to estimate SNR for same distance (200 km) Thus make the range factor 1. Thus the equation would look like :
SNRsc=20*(5/1)*((1)^4)
SNRsc=100 or 20 dB or Much better SNR.
Accuracy wise especially for angular accuracy, you can use the following expression from "Radar Homing Guidance for Tactical Missiles" bit old but AESA today still use monopulse angle tracking.
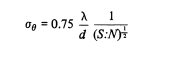
There actually addition of "Secant of beamsteering angle in radians" for taking account of beam broadening during electronic scan (yes, phased array accuracy when the radar pointing broadside or 0 deg can be different when the radar beam is pointing/steered elsewhere, due to beam broadening, caused by aperture foreshortening effect)
Suppose both radars have say 1000 TRM, the beamwidth which is the (lambda/d) notation at the equation can be substituted with :
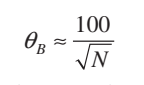
Where N is number of elements and Theta B is beamwidth in degrees. This yield you 3.16 degrees or 0.055 Radians. The constant 0.75 is apparently derived from 1/Km where Km is monopulse slope constant (1.2-1.6). Now that we have all the values needed we can do our calculations :
accuracy = 0.75*0.055*(1/(20^(1/2)))
accuracy = 0.009 Radians or 0.528 degrees for the reference radar with 13 dB SNR.
Now repeating the same for the supposed GaN radar you will have :
accuracy = 0.75*0.055*(1/(100^(1/2)))
accuracy = 0.004125 Radians or 0.236 degrees for the reference radar with 20 dB SNR.
In range of 200 km as previous calculations. This translates to angular accuracy/error of :
Radar 13 dB SNR = 0.009 * 200000
Radar 13 dB SNR acc = 1844 meter
--------
Radar 20 dB SNR = 0.004 * 200000
Radar 20 dB SNR acc = 825 meter
As you noticed, the accuracy improve quite considerably for the radar with higher power.